Les paraboles prime focus et offset
Petit aperçu :
C’est en discutant avec des OM QRV sur 1GHz 2 qu’il a été
utile de faire le point sur les paraboles.
C’est en effet un aérien très utilisé en UHF et SHF.
Les quelques notions suivantes paraîtront simplistes pour des OM connaissant
et trafiquant déjà dans ces bandes, mais pour l’expérimentateur
averti, de nombreux ouvrages sur les paraboles existent.
Nous ne décrirons alors que les principes de bases qui peuvent parfois
être nécessaires pour la compréhension de ces éléments
qui, rappelons le, deviennent de plus en plus fréquents dans notre entourage.
La fonction initiale d’une parabole est de la forme
y = a x² + b x + c
ou :
z/c² = x²/a² + y²/b²
dans l’espace.
C’est aussi une conique (ou une quadrique pour son équivalent
3D) dont les propriétés sont les suivantes :
PQ+Qf = P’Q’+Q’f = constante = 2Of
f étant le foyer de la parabole
Of étant la distance focale de la parabole
Cette propriété de la construction de la figure est intéressante
puisque le trajet entre un point du plan pi et le foyer f est constant et
égal à deux fois la distance focale après réflexion.
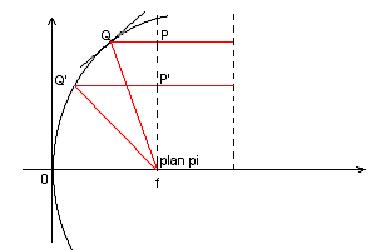
Un rayon perpendiculaire à ce plan pi et parallèle à
la droite directrice se reflétera sur la parabole et le rayon réfléchi
passera par le foyer f. Comme cette distance (PQ+Qf=P’Q’+Q’f)
est constante pour tout rayon issu de P appartenant à pi, il n’y
aura pas de déphasage en f.
C’est la propriété qui nous intéresse le plus.
Les rayons sont concentrés en f, d’où un gain important.
Remarquons au passage que ce gain est d’autant plus important que
le diamètre de la parabole est élevé.
En effet une surface effective plus importante concentre plus de rayons
d’où un gain plus élevé.
En règle générale, nous prendrons :
GdB=10log((πd/λ)²/2)
d Diamètre de la parabole
λ Longueur d’onde
Cette propriété est connue depuis longtemps, notamment en
optique : paraboles de lampes de poches, phares de voitures etc…
Les radiotélescopes sont très souvent des réflecteurs
paraboliques, ou des secteurs de paraboloïdes.
Cette antenne offrant un gain important en réception, est aussi utilisée
en émission.
Elle est par contre très directive et doit offrir un tube d’onde
de diamètre constant.
Ce n’est pas tout à fait vrai dans la pratique, où les
irrégularités du réflecteur ne peuvent être éliminées.
Il existe aussi des phénomènes de diffraction sur les bords
de la parabole.
Les sociétés de télécommunications utilisent
souvent ces antennes pour effectuer des faisceaux hertziens.
Pour des débits de 34Mbits/s, les fréquences atteignent l’ordre
de 30 GHz, pour des bonds de 20Km.
Cette fréquence élevée permet des débits importants
et des aériens dont leurs surfaces ne sont pas trop élevées.
Voyons maintenant les relations liant les angles d’ouverture, le diamètre
de la parabole et la fréquence d’émission.
Pour ce qui est de l’angle d’ouverture de la parabole, on utilise
très souvent la relation empirique suivante :
2.5 < d/Of < 2.7
Un des inconvénients majeurs est la présence de la source
au centre de la parabole.
Il fait en effet de l’ombre aux rayons émis.
De plus il n’est pas tout à fait ponctuel, et dans l’absolu
pas tout à fait sur la droite principale de l’aérien.
Les rayons qui se trouvent très prés de l’axe de la
parabole se reflètent et sont renvoyés dans la source.
Si ce champ arrive en cette source en opposition de phase, il peut influer
les émissions en cours.
La source primaire doit être placée à une distance Of
du réflecteur pour que l’onde arrivant soit en phase.
Nous prendrons la formule issue des équations de propagation de Maxwell
et des propriétés de la parabole :
Of = (2*k-1)λ/4
Et :
d = (2k-1)λsinφ/(1+cosφ)
φ = demi angle d’ouverture de la parabole
k = entier
Exemple : si φ=52° , k=28 et l=0.1m, nous obtenons d=2.68m et Of= 1.375m.
Pour des fréquences au-dessus de 3GHz, nous ne retiendrons pas cette
condition car les réglages deviennent difficiles et le foyer peut
être considéré comme lointain.
Ce type de parabole, avec la source sur l’axe principal est aussi
appelé « Prime-focus », mais est rarement installé
chez le particulier.
Un autre type de parabole est très souvent utilisé :
la parabole « offset ».
La parabole offset :
Le principe de concentration des rayons est toujours respecté pour
la parabole offset : sa forme résulte de l’intersection
d’un cône et d’un paraboloïde de révolution.
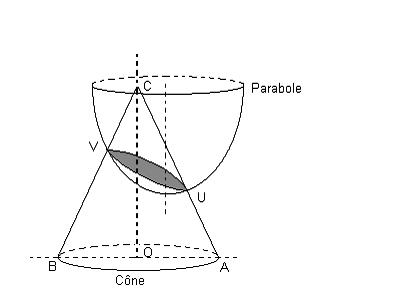
Le foyer C est alors excentré. On élimine ainsi les problèmes
dus au cône d’ombre créé par ce dernier.
De plus, grâce à cette forme, l’axe de la parabole n’a
plus besoin d’être aligné avec l’émetteur
(satellite en général).
La parabole peut être installée verticalement, ce qui évite
son remplissage d’eau de pluie ou de neige.
Pour les paraboles réceptrices du particulier, un « Low
Noise Converter » est placé au niveau du foyer.
Il amplifie le signal réfléchi sur la parabole et abaisse sa
fréquence autour du Ghz, pour le déport câble vers le
récepteur.
Pour l’utilisation en émission, il faudra bien sur tenir compte
de l’angle de déviation.
Les installations militaires ou radio TV préfèrent en général
utiliser des paraboles prime focus pour leurs liaisons.
Un peu d’info…
Suite à ces quelques notions sur les paraboloïdes elliptiques(H.I.),
je me suis plongé pendant quelques heures sur la conception d’un
petit utilitaire informatique.
En donnant λ, φ et k, ce dernier me donne l’allure d’une parabole
prime focus en 3D (s’il vous plait…).
Il permet aussi la rotation en 3D de la courbe, bien pratique pour ce faire
une vision d’ensemble (Il permet le tracé de n’importe
quelles courbes mathématiques par ailleurs).

Il me reste tout de même à l’améliorer encore un
peu pour qu’il puisse me donner l’allure d’une offset.

Ce petit programme en C permet aussi d’obtenir une bonne série
de points.
Ils peuvent être imprimés sur un support papier, et utilisés
par l’amateur pour une éventuelle conception d’un réflecteur.
Ils peuvent aussi être transférés vers un outil à
commande numérique pour l’usinage d’un moule en polystyrène
par exemple.
Pour les amateurs, de nombreuses techniques existent pour concevoir le moule.
Il faut très souvent s’armer de patience.